本文由SCY编写，转载请注明出处。

这篇文章致力于更新R绘制空间数据的方法。

本文由SCY翻译自《Spatial Data Science With Applications in R》第二章

本文由SCY翻译自《Spatial Data Science With Applications in R》第一章

本章介绍了一系列与处理空间和时空数据相关的概念，并指向后续章节，其中这些概念将会被更详细地讨论。它还介绍了一系列构成所有空间数据科学语言实现基础的开源技术。

本文由SCY原创，转载注明出处。

时间序列趋势分析

时序趋势分析是一种重要的统计技术，用于分析随时间变化的数据模式。以下是一些常用的时序趋势分析方法：

• 线性和非线性趋势分析：

  通过线性回归或非线性回归模型，可以估计时间序列数据的趋势。例如，一元线性回归可以用来估计线性趋势，而多项式回归或指数回归可以用来估计非线性趋势。

• 季节分解（Seasonal Decomposition）：

  季节分解可以分离出时序数据中的趋势、季节性和随机组成部分。例如，可以使用STL（Seasonal and Trend decomposition using Loess）或季节分解的经典方法。

• 时间序列平滑（Time Series Smoothing）：

  时间序列平滑方法，如移动平均和指数平滑，可以用来估计时间序列数据的趋势。

• 自相关和偏自相关分析（Autocorrelation and Partial Autocorrelation Analysis）：

  通过计算时间序列数据的自相关和偏自相关函数，可以识别数据中的循环模式和趋势。

• 时间序列分解（Time Series Decomposition）：

  将时间序列分解为趋势、周期和随机噪声组件，通常使用模型如X-12-ARIMA或其变体。

• 时间序列模型（Time Series Modeling）：

  ARIMA（自回归整合移动平均模型）、ETS（错误、趋势、季节性模型）和状态空间模型等可以用于分析时间序列的趋势和周期性。

• 波段分析（Wavelet Analysis）：

  波段分析可以在不同的时间尺度上识别时序数据的趋势和周期性。

• Mann-Kendall趋势检验和Sen的斜率估计：

  这些非参数方法用于检测时间序列数据的趋势并估计变化的速度。

• 突变点分析（Changepoint Analysis）：

  用于识别时间序列数据中的结构变化，例如趋势的改变或方差的改变。

• 谱分析（Spectral Analysis）：

  通过分析时序数据的频率域特性来识别周期性和趋势。

一元线性回归和Mann-Kendall检验

本文重点介绍一元线性回归和Mann-Kendall检验的原理和R语言实现步骤，以1980——2020年的降雨数据为例。

一元线性回归和Mann-Kendall检验是分析时间序列趋势的两种不同方法，它们各自有其特点和适用场景。下面是对它们的比较和联系的说明：

1. 基本原理：

一元线性回归是基于参数的统计方法，它假设数据之间存在线性关系，并试图找到描述这种关系的线性方程。它提供了估计的斜率和截距，以及相关的统计测试，以评估这种关系的显著性和强度。

Mann-Kendall检验是一种非参数的统计方法，用于检测时间序列数据中的单调趋势，而不假设数据之间的特定关系。它基于数据的秩次，而不是数据的实际值。

2. 假设：

一元线性回归通常需要满足一些基本假设，例如误差的正态性和独立性，以及数据的线性关系。当数据不满足这些假设时，线性回归的结果可能会受到影响。

Mann-Kendall检验作为非参数检验，不需要数据满足正态分布或其他分布假设，因此它对异常值和非正态数据更具鲁棒性。

3. 输出：

一元线性回归提供了详细的模型参数（例如斜率和截距）和预测值，同时也提供了模型的显著性检验结果。

Mann-Kendall检验主要提供了趋势的显著性检验结果，但不提供具体的模型参数或预测值。

4. 适用场景：

当数据具有明确的线性关系，并且满足线性回归的基本假设时，一元线性回归是一个很好的选择。

当数据可能有单调趋势，但不一定是线性的，或者当数据可能包含异常值或不满足正态分布假设时，Mann-Kendall检验可能是一个更好的选择。

5. 联系：

两者都可以用于分析时间序列数据中的趋势，但方法和假设有很大的不同。

在某些情况下，它们可以互补使用。例如，可以首先使用Mann-Kendall检验来确定是否存在显著的趋势，然后使用一元线性回归来估计趋势的具体参数。

6. 扩展：

Mann-Kendall检验可以与Sen的斜率估计结合使用，以提供趋势的斜率估计，这在一定程度上类似于一元线性回归提供的斜率估计。

一元线性回归

一元线性回归用于研究一个变量（自变量）如何线性影响另一个变量（因变量）。以下是一元线性回归的基本原理和步骤：

数学模型：

一元线性回归假设两个变量之间存在线性关系，可以用下面的方程式表示：
$$ Y = \beta_0 + \beta_1X + \varepsilon $$

其中：

• ( Y ) 是因变量的值，
• ( X ) 是自变量的值，
• ( $\beta_0$ ) 是截距项，
• ( $\beta_1$ ) 是斜率项，
• ( $\varepsilon$ ) 是误差项。

参数估计：

一元线性回归的目标是找到最佳的 ( $\beta_0$ ) 和 ( $\beta_1$ )，使得模型的预测值与实际值的差异（误差平方和，$SSE$）最小。这通常通过最小二乘法（OLS）实现，它的基本思想是最小化所有观测值的残差平方和，即：
$$SSE = \sum_{i=1}^n (Y_i - (\beta_0 + \beta_1X_i))^2 $$

通过对 $SSE$ 关于 $\beta_0$ 和 $\beta_1$ 的偏导数并令其为零，可以解得 $\beta_0$ 和 $\beta_1$ 的估计值。

显著性检验：

一旦得到了 $\beta_0$ 和 $\beta_1$ 的估计值，通常会进行假设检验来评估这些参数是否显著不为零。这涉及到计算$t$统计量和对应的$p$值。如果$p$值低于某个预定的显著性水平（通常为0.05），则认为参数是显著的。

模型评估：

模型评估通常包括计算 $R^2$ （决定系数）和调整 $R^2$，以评估模型对数据的拟合程度。$R^2$ 表示模型解释的数据变异的比例。

预测：

使用得到的 $\beta_0$ 和 $\beta_1$ 估计值，可以对新的 $X$ 值做预测，并计算预测区间，以估计预测的不确定性。

模型诊断：

模型诊断是检查模型是否满足回归分析的基本假设，例如误差的正态性、独立性和方差齐性。这可以通过残差图、正态概率图和其他诊断图来完成。

案例分析

Mann-Kendall检验和Sen斜率估计

Mann-Kendall（MK）检验和Sen的斜率估计是两种常用的非参数方法，用于分析时间序列数据中的趋势。下面是它们的基本原理介绍：

Mann-Kendall检验：

Mann-Kendall检验是一种非参数检验，用于确定一个数据序列中是否存在单调的趋势。它不需要数据满足特定的分布假设，因此对于非正态分布的数据很有用。MK检验的基本步骤如下：

1. 对于序列中的每一对数据点($x_i$, $x_j$)，计算符号统计量 ($S$)：
   $$S = \sum_{i=1}^{n-1} \sum_{j=i+1}^n \text{sign}(x_j - x_i)$$
   其中$\text{sign}(x_j - x_i)$是符号函数，如果 $x_j$ > $x_i$ 则值为 +1，如果 $x_j$ < $x_i$ 则值为 -1，如果 $x_j$ = $x_i$ 则值为 0。

2. 计算检验统计量 $U$ 和对应的 $p$ 值以判断趋势是否显著。

Sen的斜率估计：

Sen的斜率估计是一种非参数方法，用于估计数据序列中的趋势斜率。它通过计算所有可能的数据点对之间的斜率，然后取这些斜率的中位数作为趋势斜率的估计。Sen的斜率估计的基本步骤如下：

1. 对于序列中的每一对数据点$(x_i, y_i)$ 和 $(x_j, y_j)$，计算斜率：
   $$d_k = \frac{(y_j - y_i)}{(x_j - x_i)}$$
   其中 $1 \leq i < j \leq n$。

2. 从所有计算得到的斜率 $d_k$ 中，取中位数作为Sen的斜率估计：
   $$b_{\text{Sen}} = \text{median}(d_k)$$
   Sen的斜率估计可以提供一个关于时间序列数据趋势的稳健（对异常值不敏感）的估计，而Mann-Kendall检验可以提供这种趋势是否显著的证据。通常，这两种方法可以结合使用，以提供对数据趋势的全面理解。在时间序列趋势分析中，MK检验通常用于检测趋势的显著性，而Sen的斜率估计用于量化趋势的大小。

案例分析

本文由SCY原创，转载注明出处。

本文主要讲解地图可视化

本文由SCY原创，转载注明出处。

本文主要讲解ggplot2包的绘图原理及案例。

本文由SCY原创，转载注明出处。

本文主要讲解R的terra包的使用技巧，包括数据导入，批量处理，绘图，导出等内容

本文由SCY翻译自《Geocomputation with R》第十六章

综合本书的内容，引用重复出现的主题/概念，并激发未来应用和发展的方向。本章不需要先修知识。然而，如果您已经阅读并尝试了第一部分（基础）中的练习，并考虑了地理计算如何帮助您解决工作、研究或其他问题，参考了第三部分（应用）中的章节，那么您可能会从中获得更多收益。

本文由SCY翻译自《Geocomputation with R》第十五章

本章通过模拟雾绿洲（也叫lomas）的植被分布，揭示了明显受到水源供应控制的不同植被区域。这个案例研究不仅整合了前几章中的核心观点，还拓展了这些观点，帮助你更全面地掌握使用R进行地理计算的相关技能。

本文由SCY翻译自《Geocomputation with R》第十四章

• T本章要求使用下列包 (tmaptools 必须安装）:

1
2
3
4
5
6

library(sf)
library(dplyr)
library(purrr)
library(terra)
library(osmdata)
library(spDataLarge)

• 必要的数据将会在适当的时候下载。

为了方便读者并确保易于复现，我们已将下载的数据放在 spDataLarge 包中供使用。

引言

本章展示了在第一部分和第二部分学到的技能如何应用于特定领域：地理营销（有时也称为位置分析或位置智能）。这是一个广泛的研究和商业应用领域。地理营销的典型例子是如何选择一个新店的位置。这里的目标是吸引最多的顾客，最终实现最大的利润。此外，还有许多非商业应用可以利用这种技术来造福公众，例如选择新的卫生服务设施的位置。

人类对于位置分析来说是基本要素，特别是人们可能会在哪里花费时间和其他资源。有趣的是，生态学的概念和模型与用于店铺选址分析的概念和模型非常相似。动植物可以在某些“最优”位置最好地满足其需求，这些位置是基于随空间变化的变量确定的。这是地理计算和地理信息科学的一个重要优势：概念和方法可以转移到其他领域。例如，北极熊更喜欢气温较低且食物（海豹和海狮）丰富的北纬地区。同样地，人类倾向于聚集在某些地方，创造出类似于北极地区的生态位的经济位。位置分析的主要任务是基于现有数据找出这些特定服务的“最优位置”在哪里。典型的研究问题包括：

• 目标群体居住在哪里，他们经常去哪些地区？
• 竞争的商店或服务位于哪里？
• 有多少人可以轻松到达特定的商店？
• 现有的服务是否过度或不足地利用了市场潜力？
• 公司在特定地区的市场份额是多少？

本章通过一个基于实际数据的假设案例研究，演示了地理计算如何回答这些问题。

案例研究：德国自行车商店

假设您正在德国开设一家自行车连锁店。这些店铺应该位于尽可能多的潜在顾客所在的城市地区。此外，一个虚构的调查（仅用于本章，非商业用途！）表明，单身年轻男性（年龄在20到40岁之间）最有可能购买您的产品：这就是目标受众。幸运的是，您有足够的资本来开设多家店铺。但是，它们应该放在哪里呢？咨询公司（雇佣地理营销分析师的公司）通常会收取高额费用来回答此类问题。幸运的是，借助开放数据和开源软件，我们可以自己解决这些问题。以下几节将演示如何将本书前几章学到的技术应用于执行服务位置分析中的常见步骤：

• 整理来自德国人口普查的输入数据
• 将表格化的人口普查数据转换为栅格对象
• 识别人口密度较高的大都市地区
• 为这些地区下载详细的地理数据（使用osmdata从OpenStreetMap下载）
• 使用地图代数创建评分栅格，以评估不同位置的相对吸引力

尽管我们将这些步骤应用于一个特定的案例研究，但它们可以推广到许多店铺选址或公共服务提供的情景。

整理数据

德国政府提供了分辨率为1公里或100米的栅格化人口普查数据。下面的代码块用于下载、解压缩和读取1公里分辨率的数据。

1
2
3
4

download.file("https://tinyurl.com/ybtpkwxz", 
              destfile = "census.zip", mode = "wb")
unzip("census.zip") # unzip the files
census_de = readr::read_csv2(list.files(pattern = "Gitter.csv"))

请注意，census_de 数据也可以从 spDataLarge 包中获取：

1

data("census_de", package = "spDataLarge")

census_de 对象是一个包含13个变量的数据框，涵盖德国境内超过360,000个栅格单元。对于我们的工作，我们只需要其中的一个子集：东向坐标 (x)、北向坐标 (y)、居民数量（人口；pop）、平均年龄（mean_age）、女性比例（women）和平均家庭规模（hh_size）。下面的代码块从这些变量中选择并将其从德文重命名为英文，并在表格 @ref(tab:census-desc) 中进行了总结。此外，mutate() 函数被用于将值-1和-9（表示“未知”）转换为 NA。

1
2
3
4
5
6
7

# pop = population, hh_size = household size
input = select(census_de, x = x_mp_1km, y = y_mp_1km, pop = Einwohner,
                      women = Frauen_A, mean_age = Alter_D, hh_size = HHGroesse_D)
# set -1 and -9 to NA
input_tidy = dplyr::mutate(input,
  dplyr::across(.cols = c(pop, women, mean_age, hh_size), 
                .fns =  ~ifelse(.x %in% c(-1, -9), NA, .x)))

Table: Categories for each variable in census data from Datensatzbeschreibung…xlsx located in the downloaded file census.zip (see Figure @ref(fig:census-stack) for their spatial distribution).

创建人口普查栅格

在预处理之后，可以使用rast()函数将数据转换为SpatRaster对象。当将其 type 参数设置为 xyz 时，输入数据框的 x 和 y 列应该对应于正规栅格上的坐标。所有其余列（在这里是 pop、women、mean_age、hh_size）将用作栅格图层的值（请参阅图 @ref(fig:census-stack)；还可以在我们的 GitHub 存储库中的code/14-location-figures.R 文件中找到相关代码）。

1

input_ras = terra::rast(input_tidy, type = "xyz", crs = "EPSG:3035")

1
2
3
4
5
6
7
8
9
10

input_ras
#> class       : SpatRaster 
#> dimensions  : 868, 642, 4  (nrow, ncol, nlyr)
#> resolution  : 1000, 1000  (x, y)
#> extent      : 4031000, 4673000, 2684000, 3552000  (xmin, xmax, ymin, ymax)
#> coord. ref. : ETRS89-extended / LAEA Europe (EPSG:3035) 
#> source(s)   : memory
#> names       : pop, women, mean_age, hh_size 
#> min values  :   1,     1,        1,       1 
#> max values  :   6,     5,        5,       5

📌请注意，我们使用的是等面积投影（EPSG:3035；欧洲兰伯特等面积投影），即每个栅格单元的面积相同，这里是1000 x 1000平方米。由于我们主要使用诸如每个栅格单元的居民数量或女性比例等密度数据，因此每个栅格单元的面积相同非常重要，以避免“苹果与橙子比较”。请注意，在地理坐标系（CRS）中，栅格单元的面积在向极地方向不断减小，因此需要谨慎处理。

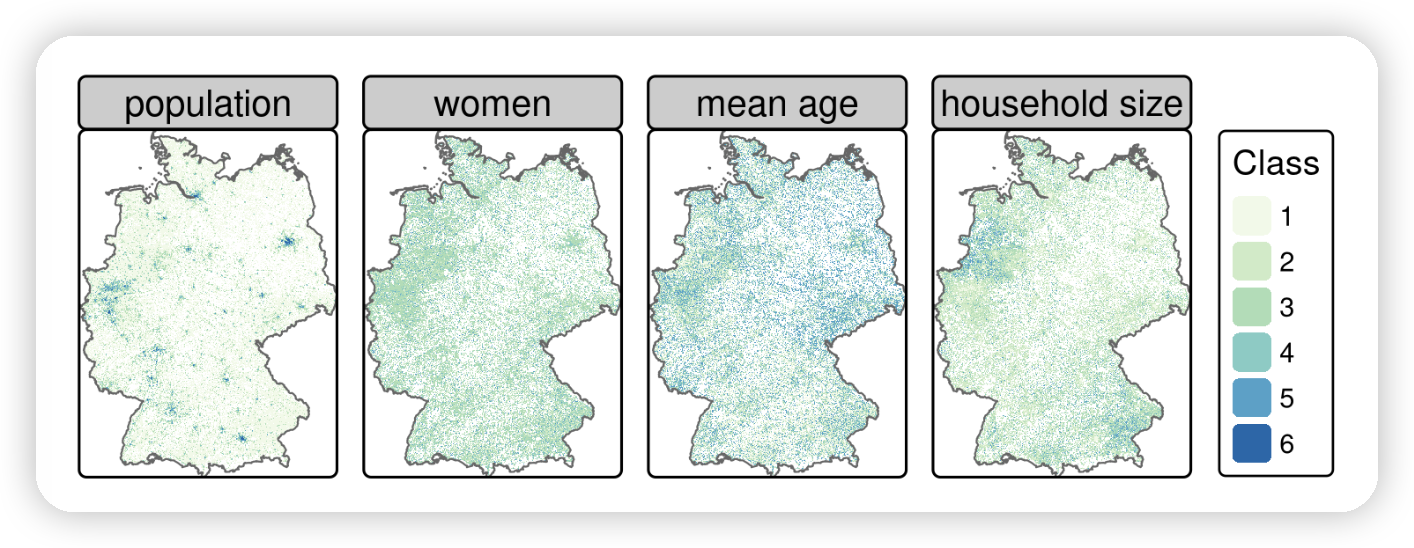
Gridded German census data of 2011 (see Table @ref(tab:census-desc) for a description of the classes).

下一步是根据前面章节提到的调查，使用 terra 函数 classify() 对存储在 input_ras 中的栅格图层的值进行重新分类。对于人口数据，我们使用类均值将类别转换为数值数据类型。假设栅格单元的值为1（‘class 1’ 中的单元包含3到250名居民），则栅格单元的人口被假定为127；如果值为2（包含250到500名居民的单元），则人口被假定为375，依此类推（请参阅上表）。对于’类别6’，栅格单元的值被选为8000名居民，因为这些单元包含的人口超过8000人。当然，这些都是对真实人口的近似值，而不是精确值。^[在这个重新分类阶段引入的潜在误差将在练习中进行探讨。]然而，这个详细级别足以划定大都市区域（请参阅下一节）。

与变量 pop 不同，该变量表示总人口的绝对估计，其他变量被重新分类为与调查中使用的权重相对应的权重。例如，变量 women 中的’类别1’代表的是人口中女性占0到40%的地区；这些地区被重新分类为较高的权重3，因为目标人群主要是男性。同样地，包含最年轻人口和最高比例的单身家庭的类别被重新分类为高权重。

1
2
3
4
5
6
7
8
9

rcl_pop = matrix(c(1, 1, 127, 2, 2, 375, 3, 3, 1250, 
                   4, 4, 3000, 5, 5, 6000, 6, 6, 8000), 
                 ncol = 3, byrow = TRUE)
rcl_women = matrix(c(1, 1, 3, 2, 2, 2, 3, 3, 1, 4, 5, 0), 
                   ncol = 3, byrow = TRUE)
rcl_age = matrix(c(1, 1, 3, 2, 2, 0, 3, 5, 0),
                 ncol = 3, byrow = TRUE)
rcl_hh = rcl_women
rcl = list(rcl_pop, rcl_women, rcl_age, rcl_hh)

请注意，我们确保了列表中重新分类矩阵的顺序与 input_ras 的元素顺序相同。例如，第一个元素在两种情况下都对应于人口。随后，for 循环\index{loop!for} 将重新分类矩阵应用于相应的栅格图层。最后，下面的代码块确保 reclass 图层与 input_ras 的图层具有相同的名称。

1
2
3
4
5

reclass = input_ras
for (i in seq_len(terra::nlyr(reclass))) {
  reclass[[i]] = terra::classify(x = reclass[[i]], rcl = rcl[[i]], right = NA)
}
names(reclass) = names(input_ras)

1
2
3
4
5

reclass
#> ... (full output not shown)
#> names       :  pop, women, mean_age, hh_size 
#> min values  :  127,     0,        0,       0 
#> max values  : 8000,     3,        3,       3

定义都市区

我们特意将大都市区域定义为面积为20平方公里且居住人口超过500,000人的像素。在这种粗分辨率下，可以通过使用 aggregate()快速创建像素。下面的命令使用参数 fact = 20 将结果的分辨率降低了20倍（回想一下，原始栅格的分辨率是1平方公里）：

1
2
3
4
5
6
7
8
9
10

pop_agg = terra::aggregate(reclass$pop, fact = 20, fun = sum, na.rm = TRUE)
summary(pop_agg)
#>       pop         
#>  Min.   :    127  
#>  1st Qu.:  39886  
#>  Median :  66008  
#>  Mean   :  99503  
#>  3rd Qu.: 105696  
#>  Max.   :1204870  
#>  NA's   :447

接下来的步骤是仅保留居住人口超过500,000人的单元格。您可以使用以下代码来实现：

1

pop_agg = pop_agg[pop_agg > 500000, drop = FALSE] 

绘制这些数据将显示出八个大都市区域。每个区域由一个或多个栅格单元组成。如果我们能够将属于同一区域的所有单元格连接起来，那将会很好。terra 的 patches() 命令正是这样的功能。随后，as.polygons() 将栅格对象转换为空间多边形，而 st_as_sf() 将其转换为 sf 对象。

1
2
3
4

metros = pop_agg |> 
  terra::patches(directions = 8) |>
  terra::as.polygons() |>
  sf::st_as_sf()

The aggregated population raster (resolution: 20 km) with the identified metropolitan areas (golden polygons) and the corresponding names.

生成的八个适合自行车店的大都市区域；请参阅 code/14-location-figures.R 以创建图表）仍然缺少名称。逆地理编码方法可以解决这个问题：根据坐标找到对应的地址。因此，提取每个大都市区域的中心坐标可以作为逆地理编码API的输入。这正是 tmaptools 包中的 rev_geocode_OSM() 函数所期望的。此外，将 as.data.frame 设置为 TRUE 将返回一个包含多列关于位置的 data.frame，包括街道名称、门牌号和城市。然而，在这里，我们只关注城市的名称。

1
2
3
4
5
6

metro_names = sf::st_centroid(metros, of_largest_polygon = TRUE) |>
  tmaptools::rev_geocode_OSM(as.data.frame = TRUE) |>
  select(city, town, state)
# smaller cities are returned in column town. To have all names in one column,
# we move the town name to the city column in case it is NA
metro_names = dplyr::mutate(metro_names, city = ifelse(is.na(city), town, city))

为了确保读者使用完全相同的结果，我们已将它们存储在 spDataLarge 中，对象名称为 metro_names。

Table: Result of the reverse geocoding.

总体而言，我们对 city 列作为大都市名称（上表）感到满意，除了一个例外，即属于杜塞尔多夫大区的费尔伯特。因此，我们将 Velbert 替换为 Düsseldorf（上图）。像 ü 这样的特殊字符可能会在后续的操作中引起问题，例如在使用 opq() 确定大都市区域的边界框时（请参见下面的内容），因此我们避免使用它们。

1
2
3
4

metro_names = metro_names$city |> 
  as.character() |>
  {\(x) ifelse(x == "Velbert", "Düsseldorf", x)}() |>
  {\(x) gsub("ü", "ue", x)}()

兴趣点

osmdata包提供了易于使用的访问OSM数据的方法。我们不是下载整个德国的商店数据，而是将查询限制在了定义好的大都市区域，以减少计算负担并且只获取感兴趣区域内的商店位置。下面的代码块使用了许多函数，包括：

• map()（tidyverse 中的 lapply()等效函数），它遍历了八个大都市名称，随后在OSM\index{OpenStreetMap}查询函数 opq() 中定义了边界框。
• add_osm_feature() 用于指定带有键值为 shop 的OSM元素（请参阅 wiki.openstreetmap.org 以获取常见的键值对列表）。
• osmdata_sf() 将OSM数据转换为空间对象（sf 类）。
• while()，如果第一次下载失败，将重复尝试（在本例中为三次）。^[有时在第一次尝试下载OSM数据时可能会失败。]

在运行此代码之前，请考虑它将下载近2GB的数据。为了节省时间和资源，我们已将名为 shops 的输出放入 spDataLarge 包中。要在您的环境中使用它，请运行 data("shops", package = "spDataLarge")。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

shops = purrr::map(metro_names, function(x) {
  message("Downloading shops of: ", x, "\n")
  # give the server a bit time
  Sys.sleep(sample(seq(5, 10, 0.1), 1))
  query = osmdata::opq(x) |>
    osmdata::add_osm_feature(key = "shop")
  points = osmdata::osmdata_sf(query)
  # request the same data again if nothing has been downloaded
  iter = 2
  while (nrow(points$osm_points) == 0 && iter > 0) {
    points = osmdata_sf(query)
    iter = iter - 1
  }
  # return only the point features
  points$osm_points
})

在我们定义的任何大都市区域中几乎不可能没有商店。以下的 if 条件仅仅检查每个区域是否至少有一家商店。如果没有的话，我们建议尝试再次为该/这些特定区域下载商店数据。

1
2
3
4
5
6

# checking if we have downloaded shops for each metropolitan area
ind = purrr::map_dbl(shops, nrow) == 0
if (any(ind)) {
  message("There are/is still (a) metropolitan area/s without any features:\n",
          paste(metro_names[ind], collapse = ", "), "\nPlease fix it!")
}

为确保每个列表元素（一个 sf 数据框）具有相同的列^[这并不是一定的，因为OSM的贡献者在收集数据时并不总是一样仔细。]，我们只保留 osm_id 和 shop 列，使用 map_dfr 循环将所有商店合并为一个大的 sf 对象。

1
2

# select only specific columns
shops = purrr::map_dfr(shops, select, osm_id, shop)

注意：shops 已经在 spDataLarge 中提供，并且可以通过以下方式访问：

1

data("shops", package = "spDataLarge")

唯一剩下的任务是将空间点对象转换为栅格。sf 对象 shops 将被转换为一个栅格，其参数（维度、分辨率、CRS）与 reclass 对象相同。重要的是，在此处使用 length() 函数来计算每个单元格中的商店数量。

因此，下面的代码块的结果是商店密度的估计（商店/平方公里）。在使用 rasterize() 之前，使用 st_transform() 来确保两个输入的CRS匹配。

1
2
3

shops = sf::st_transform(shops, st_crs(reclass))
# create poi raster
poi = terra::rasterize(x = shops, y = reclass, field = "osm_id", fun = "length")

与其他栅格图层（人口、女性、平均年龄、户籍人口）一样，poi 栅格也被重新分类为四个类别。在一定程度上，定义类别间隔是一个主观的任务。可以使用等距断点、分位数断点、固定值或其他方法。在这里，我们选择了费舍尔-詹金斯自然断点法，该方法最小化了类内方差，其结果为重新分类矩阵提供了一个输入。

1
2
3
4
5
6
7
8
9

# construct reclassification matrix
int = classInt::classIntervals(terra::values(poi), n = 4, style = "fisher")
int = round(int$brks)
rcl_poi = matrix(c(int[1], rep(int[-c(1, length(int))], each = 2), 
                   int[length(int)] + 1), ncol = 2, byrow = TRUE)
rcl_poi = cbind(rcl_poi, 0:3)  
# reclassify
poi = terra::classify(poi, rcl = rcl_poi, right = NA) 
names(poi) = "poi"

明确合适的位置

在将所有图层组合在一起之前，只剩下几个步骤：将 poi 添加到 reclass 栅格堆叠中，并将人口图层从中移除。后者的原因有两点。首先，我们已经勾勒出了大都市区域，即人口密度高于德国其他地区平均水平的地区。其次，虽然在特定的服务区域内有许多潜在的顾客可能是有优势的，但仅仅数量本身可能并不真正代表所需的目标群体。例如，高层住宅区是人口密度较高的地区，但不一定具有购买昂贵自行车配件的高购买力。

1
2
3

# remove population raster and add poi raster
reclass = reclass[[names(reclass) != "pop"]] |>
  c(poi)

与其他数据科学项目一样，数据检索和“整理”在整个工作量中占据了很大一部分。有了干净的数据，最后一步——通过将所有栅格图层相加来计算最终得分——可以在一行代码中完成。

1
2

# calculate the total score
result = sum(reclass)

例如，得分大于9的分数可能是一个适当的阈值，表示可以放置自行车店的栅格单元格；请参阅 code/14-location-figures.R）。

1
2
3
4
5
6
7
8

#> The legacy packages maptools, rgdal, and rgeos, underpinning the sp package,
#> which was just loaded, will retire in October 2023.
#> Please refer to R-spatial evolution reports for details, especially
#> https://r-spatial.org/r/2023/05/15/evolution4.html.
#> It may be desirable to make the sf package available;
#> package maintainers should consider adding sf to Suggests:.
#> The sp package is now running under evolution status 2
#>      (status 2 uses the sf package in place of rgdal)

1
2

<div class="leaflet html-widget html-fill-item-overflow-hidden html-fill-item" id="htmlwidget-841de324d41155df19a0" style="width:100%;height:415.296px;"></div>
<script type="application/json" data-for="htmlwidget-841de324d41155df19a0">{"x":{"options":{"crs":{"crsClass":"L.CRS.EPSG3857","code":null,"proj4def":null,"projectedBounds":null,"options":{}}},"calls":[{"method":"addTiles","args":["https://{s}.tile.openstreetmap.org/{z}/{x}/{y}.png",null,null,{"minZoom":0,"maxZoom":18,"tileSize":256,"subdomains":"abc","errorTileUrl":"","tms":false,"noWrap":false,"zoomOffset":0,"zoomReverse":false,"opacity":1,"zIndex":1,"detectRetina":false,"attribution":"&copy; <a href=\"https://openstreetmap.org/copyright/\">OpenStreetMap<\/a>,  <a href=\"https://opendatacommons.org/licenses/odbl/\">ODbL<\/a>"}]},{"method":"addRasterImage","args":["data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAACgAAAAoCAYAAACM/rhtAAAAM0lEQVRYhe3SMQ0AMAwEsQcb/hTSuQSaVLIR3HAJAADfqfR0wm1dEC9VevcCq+MAAIBhB20vBvBK3JZrAAAAAElFTkSuQmCC",[[52.69660085729196,13.08200261479863],[52.32107408861835,13.69815913809763]],0.8,null,null,null]},{"method":"addLegend","args":[{"colors":["darkgreen"],"labels":["potential locations"],"na_color":null,"na_label":"NA","opacity":0.5,"position":"bottomright","type":"unknown","title":"Legend","extra":null,"layerId":null,"className":"info legend","group":null}]}],"limits":{"lat":[52.32107408861835,52.69660085729196],"lng":[13.08200261479863,13.69815913809763]}},"evals":[],"jsHooks":[]}</script>

讨论和下一步

所呈现的方法是GIS的典型应用示例。我们将调查数据与基于专家知识和假设的方法相结合（定义大都市区域，定义类别间隔，定义最终得分阈值）。这种方法不如应用分析适用于科学研究，因为它可以提供基于证据的适合自行车店的区域，应该与其他信息来源进行比较。对方法的一些变更可以改进分析：

• 在计算最终得分时，我们使用了相等的权重，但其他因素，如户籍人口，可能与女性比例或平均年龄一样重要。
• 我们使用了所有兴趣点，但只有与自行车店相关的兴趣点，如自行车店、五金店、自行车、钓鱼、狩猎、摩托车、户外和运动用品店（请参阅 OSM Wiki 上可用的店铺值范围）可能会产生更精细的结果。
• 更高分辨率的数据可能会改善输出（请参阅练习）。
• 我们仅使用了有限的变量集和来自其他来源的数据，如 INSPIRE geoportal 或来自 OpenStreetMap 的自行车路径数据，可以丰富分析。
• 未考虑交互作用，如男性比例和单身户之间可能存在的关系。

简而言之，分析可以在多个方向上进行扩展。然而，它应该给您对如何在geomarketing背景下在R中获取和处理空间数据的第一印象和理解。

最后，我们必须指出，所呈现的分析仅仅是找到合适位置的第一步。到目前为止，我们已经确定了大小为1x1公里的区域，代表根据我们的调查可能适合自行车店的位置。分析的后续步骤可以是：

• 基于特定服务区域内的居民数量找到最佳位置。例如，在骑自行车的15分钟行程范围内，店铺应该为尽可能多的人提供可达性（服务区域路由）。在此过程中，我们应该考虑到远离店铺的人越远，他们实际访问店铺的可能性就越小（距离衰减函数）。
• 此外，考虑竞争对手也是一个好主意。也就是说，如果已经有一家自行车店在所选位置附近，可能的顾客（或销售潜力）应该在竞争对手之间分配。
• 我们需要找到适合并且价格合理的房地产，例如在可访问性、停车位的可用性、过路人的期望频率、有大窗户等方面。

练习

E1. 首先，您需要从提供的链接下载包含居民信息的CSV文件（以100米单元格分辨率）。请注意，解压缩后的文件大小为1.23 GB。您可以使用readr::read_csv将其读入R中。在具有16 GB RAM的机器上，这需要30秒钟。data.table::fread()可能会更快，它返回一个data.table()类的对象。使用dplyr::as_tibble()将其转换为tibble。构建一个居民栅格，将其聚合到1 km的单元格分辨率，并将其与我们使用类平均值创建的居民栅格（inh）进行比较。

E2. 假设我们的自行车店主要向老年人销售电动自行车。相应地更改年龄栅格，重复剩余的分析，并将更改与我们的原始结果进行比较。